개요
이 문서에서는 GLM, GEE, GLMM, Cox 모델에 대한 개요와 이를 jstable 패키지와 더불어 활용하는 방법을 소개합니다.
1. GLM
GLM의 개요
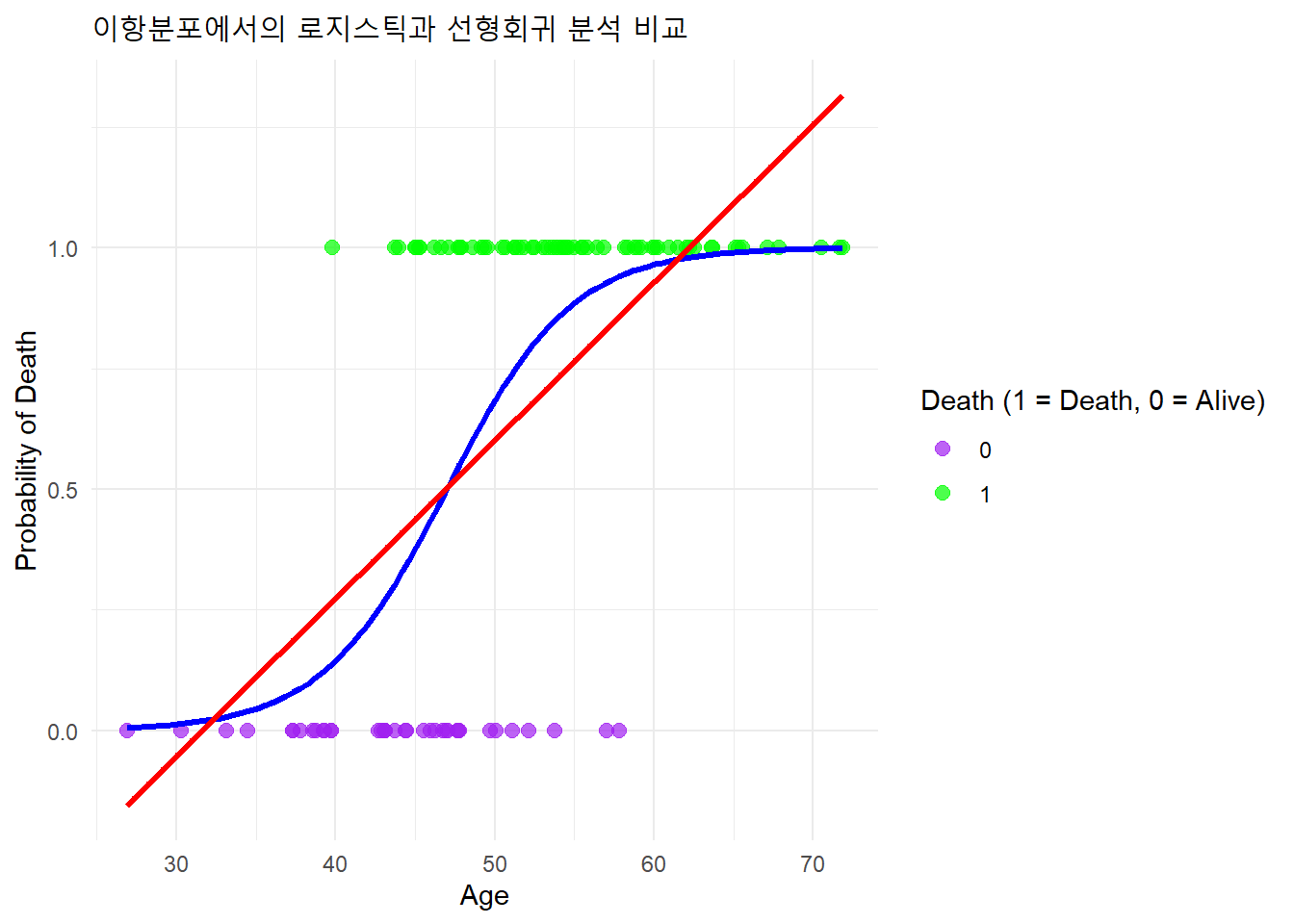
GLM은 Generalized Linear Model의 약자로 일반화 선형 모델을 의미합니다. 기존의 선형 회귀 모델에서는 반응 변수가 정규 분포를 따라야한다는 가정이 필요하지만, 현실에서는 그렇지 않은 경우가 많습니다. GLM은 이러한 경우에도 사용하기 위해 만들어진 모델입니다. 정규 분포가 아닌 흔한 예시로는 이항분포, 포아송 분포 등이 있습니다. 나이에 따른 생존 상태(생존은 1, 사망은 0)인 이항분포 반응변수를 간단한 예시로 들어보겠습니다. 일반적 선형회귀 모델과 GLM을 통해 로지스틱 회귀 분석을 한 결과를 비교해보았습니다.
일반적인 선형 회귀 함수를 적용했을 때 나이가 어린 경우에는 사망 확률이 음수가 나오며, 고령인 경우 사망 확률이 1이 넘는 등의 문제가 발생합니다. 반면, GLM(로지스틱 회귀모형)을 적용하면 모든 나이에서 사망 확률이 0에서 1사이가 됨을 알 수 있습니다.
GLM을 적용하기 위한 데이터의 조건
이항 분포에 대해 GLM을 적용하였지만, 모든 데이터에 GLM을 적용할 수 있는 것은 아닙니다. GLM을 적용하기 위한 조건에 대해 알아보겠습니다.
반응변수의 분포
반응 변수의 분포 형태가 Exponential family(지수 분포군)를 따를 때 GLM을 적용할 수 있습니다. Exponential family는 아래와 같은 수식으로 나타낼 수 있습니다. \[
f(y | \theta, \phi) = \exp\left( \frac{y\theta - b(\theta)}{\phi} + c(y, \phi) \right)
\] 여기서\(y\)는 반응 변수 \(\theta\)는 정규화 매게 변수, \(\phi\)는 분산을 나타냅니다. 이항분포를 예시로 생각해보겠습니다. 이항분포의 경우 성공 확률 \(p\)로 정의되며 아래 함수의 경우 다음과 같이 지수 분포군 함수로 변환이 가능합니다.
\[
P(Y = y) = \binom{n}{y} p^y (1 - p)^{n - y}
\] \[
P(Y = y) = \binom{n}{y} \exp\left( y \log\left( \frac{p}{1 - p} \right) + n \log(1 - p) \right)
\] 위와 같이 Exponential family로 변형이 가능한 다른 흔한 분포로는 포아송 분포, 감마 분포 등이 있습니다. Exponential Family로 변형이 가능한 분포의 경우, 지수함수의 특성으로 최대우도 추정(Maximum Likelihood Estimation)을 효율적 계산을 통해 할 수 있으며, 링크함수를 통해 선형 예측을 쉽게 할 수 있다는 장점이 있습니다.
링크 함수
Exponential family 함수의 경우 지수형태로 존재하기 때문에 곧바로 선형 회귀 분석을 할 수는 없습니다. 선형 회귀 분석과 Exponential family를 연결하기 위한 함수가 필요한데, 이를 링크함수라 부릅니다. 링크 함수를 통해 반응 변수의 평균과 예측 변수의 선형 관계를 나타낼 수 있습니다. 반응변수의 분포가 지수 분포군에 있을 때 링크함수를 사용할 수 있으며 이항 분포의 경우 예시는 이와 같습니다. 아래 함수를 적용하면 선형 관계의 그래프를 얻을 수 있습니다. 함수를 적용하니 평소에 알던 선형 회귀의 형태로 식이 나타나는 것을 알 수 있습니다. \[ \log\left( \frac{1 - \mu}{\mu} \right) = X\beta \]
관측치 독립
GLM을 적용하기 위해서는 관측치들이 독립되어 합니다. 예를 들어, 한 사람의 혈압을 반복측정하는 경우 관측치들이 독립되어 있지 않기 때문에 다른 모델을 사용하여야 합니다. 이 경우에 대해서는 문서의 아래 내용에서 다루도록 하겠습니다.
GLM table 해석하기
jstable 패키지를 사용하여 이항 분포와 가우스 분포의 GLM 모델의 결과를 직관적인 표로 만들 수 있습니다. 아래 코드는 R에서 기본으로 제공되는 mtcars 데이터를 사용하여과 이항 회귀 모델을 만들고 결과를 표로 나타낸 것입니다. 이항분포를 가지는 am(자동미션 =0, 수동미션 =1)을 wt(차량무게), hp(마력)을 통해 예측하는 GLM에 대해 알아보겠습니다.
binomial_model <- glm(am ~ wt + hp, family = binomial, data = mtcars)
glmshow.display(binomial_model, decimal = 2)$first.line
[1] "Logistic regression predicting am\n"
$table
crude OR.(95%CI) crude P value adj. OR.(95%CI) adj. P value
wt "0.02 (0,0.3)" "0.005" "0 (0,0.13)" "0.008"
hp "0.99 (0.98,1)" "0.181" "1.04 (1,1.07)" "0.041"
$last.lines
[1] "No. of observations = 32\nAIC value = 16.0591\n\n"
attr(,"class")
[1] "display" "list" 이항 분포의 glm에 대하여 첫줄에서는 로지스틱 회귀 분석을 사용했음을 알 수 있습니다. 테이블 출력 결과를 통해 wt 변수는 p-value가 0.0001로 유의미하게 미션의 종류에 영향을 미치는 것을 알 수 있습니다. Crude OR 변수를 통해 차량 무게 변수가 1이 증가할때마다 수동미션을 가질 odds 비율이 98프로 씩 감소한다는 것을 알 수 있습니다. Adjusted OR 변수가 0이라는 것을 통해 마력 변수를 보정했을 경우에 Odds 비율이 더 강하게 연관되어 있다는 것을 알 수 있으며, adjusted p value또한 유의미하다는 것을 확인 할 수 있습니다. hp의 경우 OR과 p value를 통해 관련이 적음을 유추할 수 있습니다. 마지막 줄에서는 총 몇 개의 관측치가 있었는지, 그리고 AIC 수치(낮을 수록 더 좋은 모델)를 알 수 있습니다.
gaussian_model <- glm(mpg~cyl + disp, data = mtcars)
glmshow.display(gaussian_model, decimal = 2)$first.line
[1] "Linear regression predicting mpg\n"
$table
crude coeff.(95%CI) crude P value adj. coeff.(95%CI) adj. P value
cyl "-2.88 (-3.51,-2.24)" "< 0.001" "-1.59 (-2.98,-0.19)" "0.034"
disp "-0.04 (-0.05,-0.03)" "< 0.001" "-0.02 (-0.04,0)" "0.054"
$last.lines
[1] "No. of observations = 32\nR-squared = 0.7596\nAIC value = 167.1456\n\n"
attr(,"class")
[1] "display" "list" 정규분포를 나타내는 데이터에 대해서도 적용해보겠습니다.첫줄에서는 정규분포에 대하여 선형 회귀 분석을 사용했음을 알 수 있고, 해당하는 p value 들 그리고 선형 회귀의 경우 OR 대신 Coeffecient를 제공함을 알 수 있습니다. 해당 테이블을 통해 cyl(실린더의 갯수)변수는 mpg(연비)에 유의미한 영향을 미치는 것을 알 수 있습니다. disp(배기량)변수는 보정 전에는 영향이 있어 보였으나 보정 이후 0.05보다 크기 때문에 통계적으로 유의미한 영향을 미치지 않는 것을 알 수 있습니다.
2. GEE
GEE(Generalized Estimating Equations)는 GLM에서 반복 측정 혹은 군집화 데이터와 같이 상관된 데이터를 처리하기 위해 만들어진 확장된 모델입니다. GLM의 경우 링크 함수를 통한 선형 회귀 분석을 하기 때문에 기본적으로 관측치들 간의 상관관계가 없어야 한다는 선형 회귀분석의 기본 가정을 따르게 됩니다. 하지만 실제 데이터의 경우(반복된 혈압의 측정, 같은 병원 내 환자들)과 같은 반복, 군집 데이터들을 통해 반응 변수를 분석해야 하는 경우가 많습니다. 나이별 환자의 혈압 측정을 예시로 생각해보겠습니다. 이를 일반적인 GLM 모형에 적용한다면(여기서 \(g\) 는 링크 함수, \(X\)는 종속 변수를 나타냅니다.), 같은 환자에서 반복된 혈압 측정치들이 모두 독립적이라는 가정을 필요로 합니다.
\[ g(\mu_{i}) = X_{i} \beta \]
잠시 예시를 살펴보겠습니다.
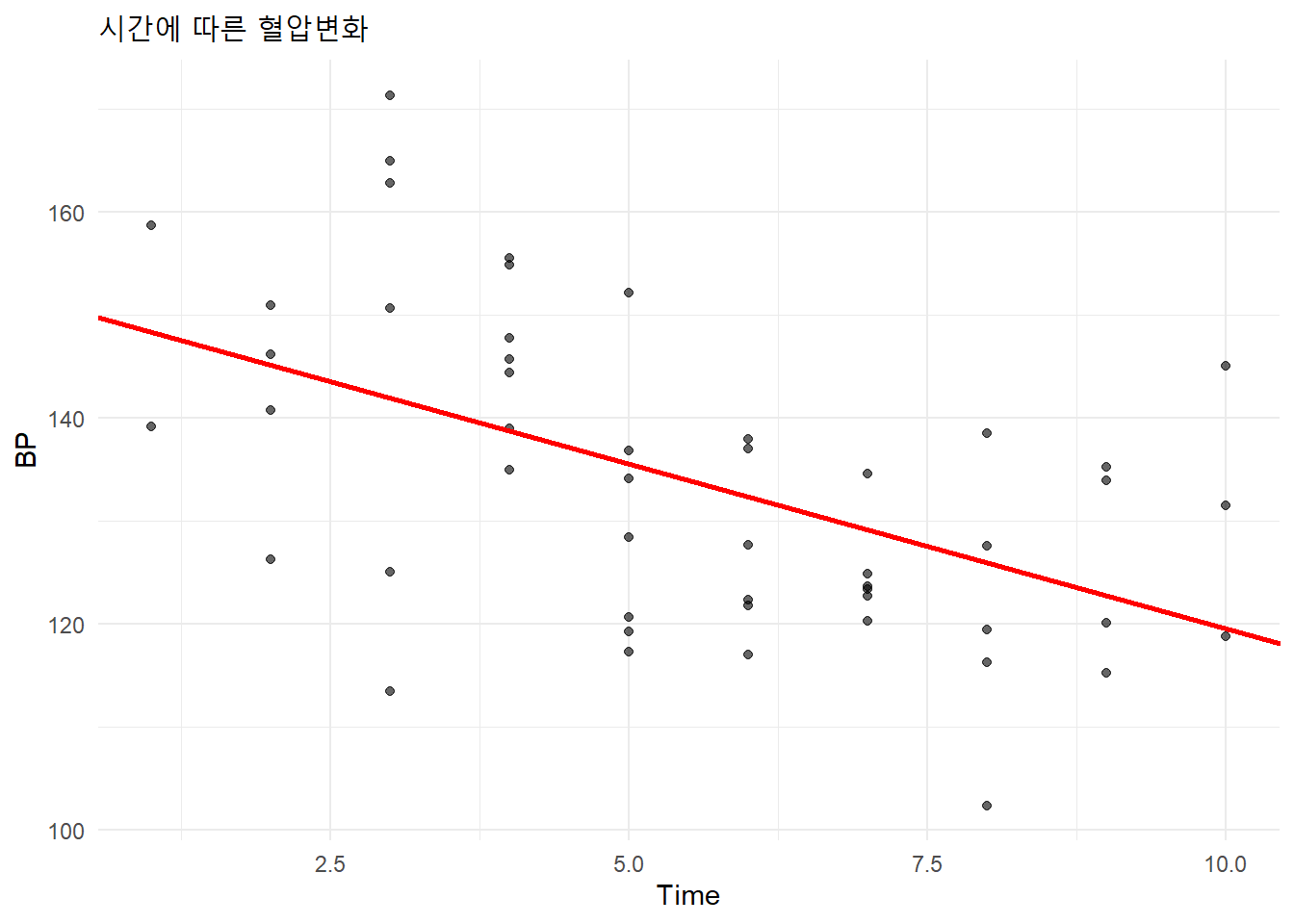
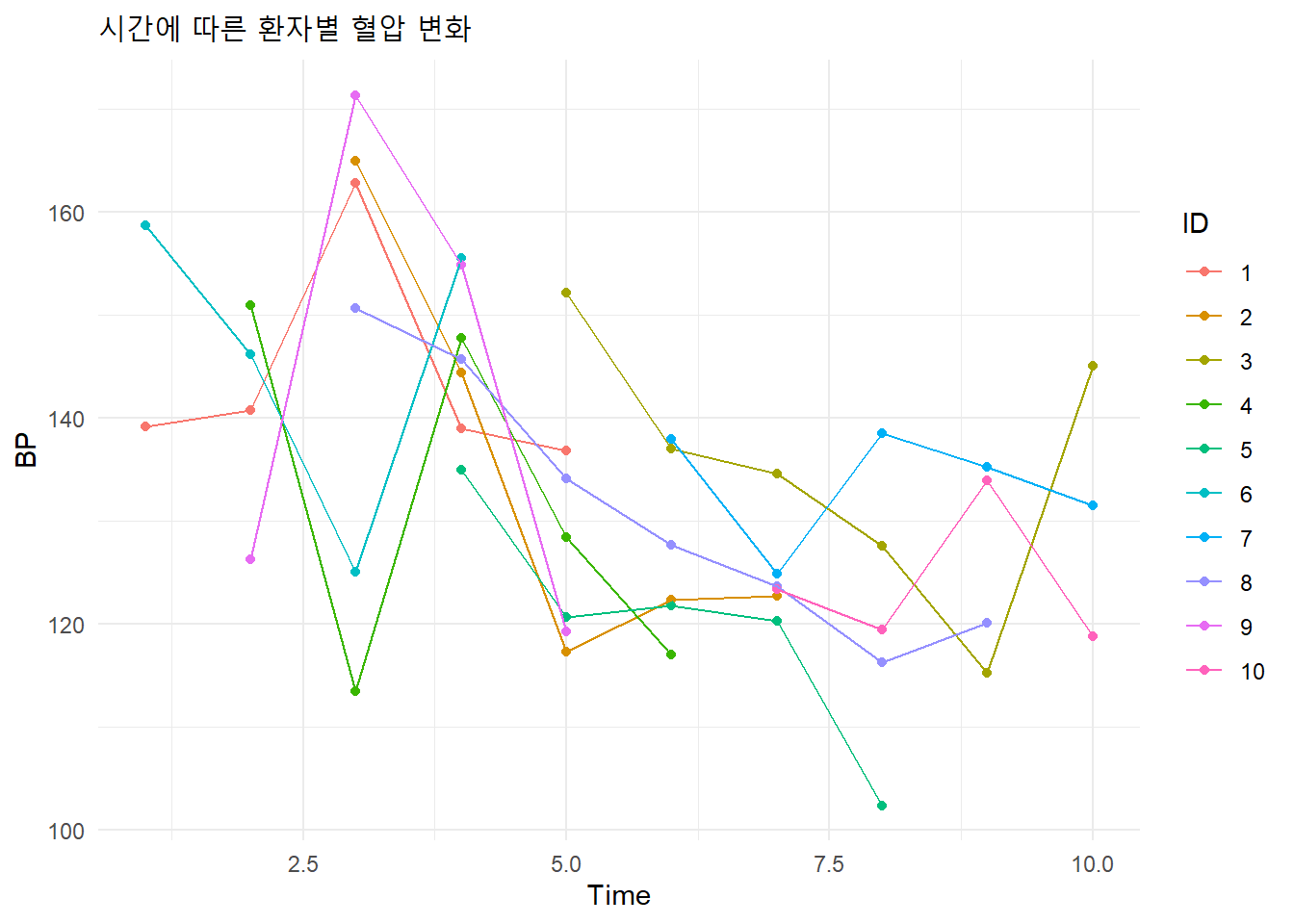
시간에 따른 혈압의 변화를 살펴보았을 떄, 같은 환자에게 반복측정되었다는 사실을 반영하지 않고 데이터를 바라보았을 때는 시간이 지날수록 혈압이 감소한다는 결론을 얻을 수 있습니다. 하지만 환자별로 살펴본다면 실제로는 제 각각의 환자들에 대해서는 시간과 유의미한 관계가 있다고 보기는 힘들다는 것을 알 수 있습니다. 이는 전체 분석을 할 때 군집 데이터의 특성을 GLM은 반영하지 않기 때문임을 알 수 있습니다. 반복측정된 데이터들간에는 상관관계가 있다는 사실을 반영한 새로운 측정방식이 필요하다는 것을 알 수 있습니다. 이러한 상관관계를 반영한 모델은 다음과 같이 쓸 수 있습니다:
\[ g(\mu_{ij}) = X_{ij} \beta \] 여기서 \(X_{ij}\)는 \(i\)번째 환자의 \(j\)번째 관측치를 나타냅니다.( \(g(\mu_{ij})\)의 경우 혈압압). 간단한 예시 적용을 위해, \(X_{ij1}\)를 환자 \(i\)의 나이, \(X_{ij2}\)를를 치료여부부 (1 = 치료군, 0 = 대조군),\(X_{ij3}\)를 혈압, \(X_{ij4}\)를 -시간(측정 시점)이라 가정해보겠습니다. \[ g(\mu_{ij}) = \beta_0 + \beta_1 \times \text{나이}_{i} + \beta_2 \times \text{치료여부}_{i} + \beta_3 \times \text{시간}_{i} \] 여기서 \(\beta_0, \beta_1, \beta_2, \beta_3,\beta_4\) (계수)는 모든 환자에 대해 일정하므로, 개인 또는 시간점에 따라 변하지 않습니다. \(X_{ij}\) (예측 변수)는 환자와 시간점에 따라 다릅니다.
GLM과 GEE의 공분산 차이
데이터간의 상관관계가 반영된다는 점에서 결과적으로 GEE는 복잡한 공분산을 반영하고 있다는 것을 알 수 있습니다.
GLM의 경우 관측치들이 독립이라는 가정이 있기 때문에 공분산 행렬이 대각행렬입니다. 반면 GEE의 경우 관측치들이 상관관계가 있다는 가정을 따르기 때문에 공분산 행렬이 대각행렬이 아닌 다른 형태를 가질 수 있습니다. 따라서 GLM에서의 공분산 행렬은 \(V_i = \phi \cdot W_i\)와 같은 구조에서 \(W_i\)는 대각행렬이 되며, GEE에서의 공분산 행렬은 \(V_i = \phi \cdot A_i^{1/2} R(\alpha) A_i^{1/2}\)와 같은 구조에서 \(A_i\)는 대각 가중치 행렬의 형태를 따르나, 상관관계를 반영하는 \(R(\alpha)\)라는 상관행렬이 있게 됩니다. 공분산과 앞선 회귀식을 모두 반영하면 GLM 과 GEE는 모두 아래의 수식과 같은 형태를 띄게 되며, \(V_i\)에서 그 차이가 나타납니다. \[ Y_i = g^{-1}(X_i^T \beta) + \epsilon_i \quad \text{with} \quad \epsilon_i \sim N(0, V_i) \]
GEE table 해석하기
jstable 패키지를 사용하여 군집 데이터의 GEE적용 후 결과 해석에 대해 알아보겠습니다. 아래 코드는 R에서 제공되는 geepack의 dietox 데이터를 이용하여 돼지의 체중을 예상하는 모델을 만드는 예시입니다. 시간과 구리 보충제 상태가 돼지의 체중에 미치는 영향을 분석해보겠습니다. 군집 데이터의 특성을 반영하여, 돼지별 데이터를 분석하였음을 코드에서도 알 수 있습니다.
library(geepack) ## for dietox data
data(dietox)
dietox$Cu <- as.factor(dietox$Cu)
dietox$ddn <- as.numeric(rnorm(nrow(dietox)) > 0)
gee01 <- geeglm (Weight ~ Time + Cu , id = Pig, data = dietox, family = gaussian, corstr = "ex")
geeglm.display(gee01)$caption
[1] "GEE(gaussian) predicting Weight by Time, Cu - Group Pig"
$table
crude coeff(95%CI) crude P value adj. coeff(95%CI)
Time "6.94 (6.79,7.1)" "< 0.001" "6.94 (6.79,7.1)"
Cu: ref.=Cu000 NA NA NA
035 "-0.59 (-3.73,2.54)" "0.711" "-0.84 (-3.9,2.23)"
175 "1.9 (-1.87,5.66)" "0.324" "1.77 (-1.9,5.45)"
adj. P value
Time "< 0.001"
Cu: ref.=Cu000 NA
035 "0.593"
175 "0.345"
$metric
crude coeff(95%CI) crude P value
NA NA
Estimated correlation parameters "0.775" NA
No. of clusters "72" NA
No. of observations "861" NA
adj. coeff(95%CI) adj. P value
NA NA
Estimated correlation parameters NA NA
No. of clusters NA NA
No. of observations NA NA 해석을 위해 jstable 패키지를 사용하여 결과를 표로 나타내었습니다. 시간의 p-value를 확인하였을 때, 시간은 돼지 체중 증가에 유의미한 영향을 미치고 있다고 할 수 있으며, 계수를 보았을 때 단위 시간당 체중이 6.94만큼 증가한다고 추정할 수 있습니다. 구리 보충제의 경우 두가지 종류의 보충제 모두 통계적으로 유의미한 영향을 미치지 않는다고 해석할 수 있습니다. Metric 부분에서는 모델의 상관구조와 관련된 정보를 알 수 있습니다. Estimated correlation parameters의 경우 같은 군집의 시간에 따른 관측값들 사이의 상관관계를 나타내며, 0.775는 높은 상관관계를 의미합니다. 아래의 cluster 와 observation에서는 총 72마리의 돼지에 대하여 861개의 관측치로 분석을 했음을 알 수 있습니다.
gee02 <- geeglm (ddn ~ Time + Cu , id = Pig, data = dietox, family = binomial, corstr = "ex")
geeglm.display(gee02)$caption
[1] "GEE(binomial) predicting ddn by Time, Cu - Group Pig"
$table
crude OR(95%CI) crude P value adj. OR(95%CI) adj. P value
Time "1.01 (0.97,1.05)" "0.609" "1.01 (0.97,1.05)" "0.615"
Cu: ref.=Cu000 NA NA NA NA
035 "1.2 (0.91,1.58)" "0.198" "1.2 (0.91,1.58)" "0.199"
175 "1.21 (0.91,1.61)" "0.189" "1.21 (0.91,1.61)" "0.19"
$metric
crude OR(95%CI) crude P value adj. OR(95%CI)
NA NA NA
Estimated correlation parameters "-0.022" NA NA
No. of clusters "72" NA NA
No. of observations "861" NA NA
adj. P value
NA
Estimated correlation parameters NA
No. of clusters NA
No. of observations NA 이번에는 이항분포를 사용하여 돼지의 체중 증가에 대한 모델을 만들어보았습니다. 이전 코드와는 다르게 family에 binomial을 입력하였으며, ddn은 임의로 0,1이 있는 이항분포 변수이며 이를 시간과 구리 보충제 상태로 예측하는 모델입니다. 이항분포이기 때문에 회귀계수 대신 OR이 있는 것을 알 수 있습니다. 변수들 모두 p-value가 통계적으로 의미 있는 수준은 아니라는 것을 알 수 있습니다. ddn이 임의 변수이기 때문에 시간이나 구리 보충제 여부에 따른 오즈비가 1에 가까울 것일 거라고 추측할 수 있고, 실제로 그러한 결과를 보여줍니다.
3. Mixed-Effects Model
앞선 데이터 분석에서 다음과 같은 의문이 생길 수 있습니다. 돼지마다 체중에 대한 기초 수준이 다를텐데, GEE의 경우에는 그러한 부분이 반영되지 않아아 이를 어떻게 해결해야할지에 대한 고민이 생길 것입니다. 이를 위해 임의 효과라는 것을 적용하여 각 군집에 대한 고유한 변동을 설명할 수 있습니다. 군집간의 기초 수준뿐만 아니라, 군집 내의 기울기 또한 달라질 수 있다는 것을 반영하는 형태로 수식을 써볼 수 있겠습니다. \[ y_{ij} = \beta_0 + \beta_1 X_{1ij} + \beta_2 X_{2ij} + (u_{i0} + u_{i1} X_{1ij}) + \epsilon_{ij} \] 여기서 \(u_{i0}\)는 군집 \(i\)의 기초 수준을 나타내며, \(u_{i1}\)은 군집 \(i\)의 기울기를 나타냅니다. 의학통계를 예시로, 다양한 병원에서 연구를 진행하였다하면 \(u_{i0}\)는 병원의 기초 수준 차이(환자들의 평균 초기 상태)들을 반영할 수 있으며 \(u_{i1}\)는 병원에서 특정 변수에 따른 반응 차이(일부 병원에서는 고령 환자의 시술에 미숙)을 반영할 수 있습니다. 이러한 Mixed-Model또한 앞서 보았던 링크함수를 사용하면 다양한 분포에 대하여 더 일반화된 Mixed-model인 GLMM(Generalized Linear Mixed Model)을 만들 수 있습니다.
jstable 패키지를 사용한 LMM table만들기
아래 코드는 R에서 제공되는 geepack의 dietox 데이터를 이용하여 돼지의 체중을 예상하는 모델을 만드는 예시입니다. GEE에서와 다르게 각 돼지별 체중의 차이가 다르다는 점을 반영한 모델을 만들어볼 것입니다.
library(lme4)
l1 <- lmer(Weight ~ Time + Cu + (1|Pig), data = dietox)
lmer.display(l1, ci.ranef = T)boundary (singular) fit: see help('isSingular')
boundary (singular) fit: see help('isSingular')Computing profile confidence intervals ...$table
crude coeff(95%CI) crude P value adj. coeff(95%CI)
Time 6.94 (6.88,7.01) 0.0000000 6.94 (6.88,7.01)
Cu: ref.=Cu000 <NA> NA <NA>
035 -0.58 (-4.67,3.51) 0.7811327 -0.84 (-4.47,2.8)
175 1.9 (-2.23,6.04) 0.3670740 1.77 (-1.9,5.45)
Random effects <NA> NA <NA>
Pig 40.34 (28.08,54.95) NA <NA>
Residual 11.37 (10.3,12.55) NA <NA>
Metrics <NA> NA <NA>
No. of groups (Pig) 72 NA <NA>
No. of observations 861 NA <NA>
Log-likelihood -2400.8 NA <NA>
AIC value 4801.6 NA <NA>
adj. P value
Time 0.0000000
Cu: ref.=Cu000 NA
035 0.6527264
175 0.3442309
Random effects NA
Pig NA
Residual NA
Metrics NA
No. of groups (Pig) NA
No. of observations NA
Log-likelihood NA
AIC value NA
$caption
[1] "Linear mixed model fit by REML : Weight ~ Time + Cu + (1 | Pig)"고정효과인 Time과 Cu 에 대해서는 이번에도 시간만 통계적으로 유의미한 변수로 나왔으며, 체중의 증가에 통계적으로 유의미한 영향을 미치는 것을 알 수 있습니다. 이번에는 임의 효과에 대해서 조금 더 자세히 알아보겠습니다. 돼지 데이터에서 임의 효과의 분산은 40.34로 나왔습니다. 이는 돼지마다 체중의 차이가 크다는 것을 알 수 있으며, 11.37이라는 잔차는 돼지별 임의 효과를 반영한 후에도 남는 체중의 변동이 있음을 설명합니다.
l2 <- glmer(ddn ~ Weight + Time + (1|Pig), data= dietox, family= "binomial")boundary (singular) fit: see help('isSingular')lmer.display(l2)boundary (singular) fit: see help('isSingular')
boundary (singular) fit: see help('isSingular')
boundary (singular) fit: see help('isSingular')$table
crude OR(95%CI) crude P value adj. OR(95%CI) adj. P value
Weight 1 (1,1.01) 0.7020746 1 (0.98,1.02) 0.8041261
Time 1.01 (0.97,1.05) 0.6358656 1.03 (0.9,1.17) 0.7088793
Random effects <NA> NA <NA> NA
Pig 0 NA <NA> NA
Metrics <NA> NA <NA> NA
No. of groups (Pig) 72 NA <NA> NA
No. of observations 861 NA <NA> NA
Log-likelihood -596.49 NA <NA> NA
AIC value 1200.98 NA <NA> NA
$caption
[1] "Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) : ddn ~ Weight + Time + (1 | Pig)"이항 분포를 가지는 변수에는 GLM과 비슷한 방식으로 일반화 된 방식인 GLMM이 적용이 가능합니다. ddn의 경우 임의로 형성된 변수이기 때문에 통계적으로 유의미하지 않은 고정 변수들을 확인할 수 있으며 OR모두 1에 가깝다는 것을 확인할 수 있습니다. 임의효과인 돼지의 분산의 경우 앞선 LMM보다 낮게 나왔습니다. 이는 0과 1만 가지는 이항데이터를 다루기 때문에, 돼지 간의 기초 수준 차이가 연속형 데이터처럼 크게 반영되지 않았기 떄문일 것입니다.
4. Cox model with frailty, cluster options
Cox model은 생존분석을 위한 모델로, 시간에 따른 사건의 발생을 예측하는 모델입니다. 이전에 다룬 GLM, GEE, LMM과 마찬가지로 Cox model도 frailty와 cluster 옵션을 사용하여 군집 데이터를 다룰 수 있습니다. 이번에도 jstable을 활용하여 분석 결과를 같이 보겠습니다. R에서 제공하는 survival library의 lung 데이터를 사용하여 Cox model을 만들어보겠습니다.
inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
1 3 306 2 74 1 1 90 100 1175 NA
2 3 455 2 68 1 0 90 90 1225 15
3 3 1010 1 56 1 0 90 90 NA 15
4 5 210 2 57 1 1 90 60 1150 11
5 1 883 2 60 1 0 100 90 NA 0
6 12 1022 1 74 1 1 50 80 513 0cluster 옵션을 사용한 Cox model
lung의 데이터는 228명의 환자에 대한 생존 데이터를 포함하고 있습니다. ECOG와 나이에 따른 폐암 환자의 생존을 예측하는 모델을 만들고 싶은데, 같은 병원에서 치료를 받게 되면 병원의 비슷한 프로토콜 등에 영향을 받아 비슷한 치료 결과를 보일 수 있습니다. 따라서, 같은 병원 내의 환자들의 상관관계를 고려하여 만들고 싶을 때 cluster 옵션을 사용할 수 있습니다.
fit1 <- coxph(Surv(time, status) ~ ph.ecog + age, cluster = inst, lung, model = T)
cox2.display(fit1)$table
crude HR(95%CI) crude P value adj. HR(95%CI) adj. P value
ph.ecog "38.34 (38.32,38.36)" "< 0.001" "33.03 (33,33.06)" "< 0.001"
age "14.67 (14.46,14.88)" "0.007" "5.59 (4.73,6.61)" "0.085"
$ranef
[,1] [,2] [,3] [,4]
cluster NA NA NA NA
inst NA NA NA NA
$metric
[,1] [,2] [,3] [,4]
<NA> NA NA NA NA
No. of observations 226.000 NA NA NA
No. of events 163.000 NA NA NA
AIC 1463.797 NA NA NA
$caption
[1] "Marginal Cox model on time ('time') to event ('status') - Group inst"table의 결과를 보았을 때 ecog는 환자의 생존에 강한 영향을 미치며 통계적으로도 유의미하다는 것을 알 수 있습니다. age 변수의 경우 조정되지 않은 모델에서는 유의미한 위험 요인으로 나타났지만, ecog를 조정한 이후에는 통계적으로 유의미하지 않았다는 것을 확인할 수 있습니다.
frailty 옵션을 사용한 Cox model
같은 병원 내의 환자들간의 상관관계 외에 병원간 차이를 고려하고 싶을 수도 있습니다. 일부 병원은 다른 병원보다 더 좋은 생존 결과를 가지고 있을 수 있기 때문에, 이에 따른 변수를 frailty 옵션을 사용해서 고려합니다.
fit2 <- coxph(Surv(time, status) ~ ph.ecog + age + frailty(inst), lung, model = T)
cox2.display(fit1)$table
crude HR(95%CI) crude P value adj. HR(95%CI) adj. P value
ph.ecog "38.34 (38.32,38.36)" "< 0.001" "33.03 (33,33.06)" "< 0.001"
age "14.67 (14.46,14.88)" "0.007" "5.59 (4.73,6.61)" "0.085"
$ranef
[,1] [,2] [,3] [,4]
cluster NA NA NA NA
inst NA NA NA NA
$metric
[,1] [,2] [,3] [,4]
<NA> NA NA NA NA
No. of observations 226.000 NA NA NA
No. of events 163.000 NA NA NA
AIC 1463.797 NA NA NA
$caption
[1] "Marginal Cox model on time ('time') to event ('status') - Group inst"table의 결과를 보았을 때 ecog와 age가 생존에 미치는 영향은 앞선 cluster 옵션을 이용했을 때와 비슷한 것을 확인할 수 있습니다.
mixed effect를 사용한 Cox model
다층 구조나 복잡한 데이터 구조를 처리하고 싶은 경우 frailty 옵션만으로 부족할 수 있습니다. 예를 들어, 병원 간의 기초 수준 차이와 성별에 따른 기초 위험이 차이가 나는 것을 반영한 모델을 만들고 싶을 수 있습니다. 해당 경우 coxme함수를 이용할 수 있습니다.
library(coxme)
fit <- coxme(Surv(time, status) ~ ph.ecog + age + (1|inst)+(1|sex), lung)
coxme.display(fit) Warning in formula.character(object, env = baseenv()): Using formula(x) is deprecated when x is a character vector of length > 1.
Consider formula(paste(x, collapse = " ")) instead.
Warning in formula.character(object, env = baseenv()): Using formula(x) is deprecated when x is a character vector of length > 1.
Consider formula(paste(x, collapse = " ")) instead.$table
crude HR(95%CI) crude P value adj. HR(95%CI) adj. P value
ph.ecog "1.66 (1.32,2.09)" "< 0.001" "1.63 (1.3,2.05)" "< 0.001"
age "1.02 (1,1.04)" "0.043" "1.01 (0.99,1.03)" "0.234"
$ranef
[,1] [,2] [,3] [,4]
Random effect NA NA NA NA
inst(Intercept) 0.02 NA NA NA
sex(Intercept) 0.14 NA NA NA
$metric
[,1] [,2] [,3] [,4]
<NA> NA NA NA NA
No. of groups(inst) 18 NA NA NA
No. of groups(sex) 2 NA NA NA
No. of observations 226 NA NA NA
No. of events 163 NA NA NA
$caption
[1] "Mixed effects Cox model on time ('time') to event ('status') - Group inst, sex"Reuse
Citation
@online{jo2024,
author = {Jo, Hyungwoo},
title = {Jstable을 {이용한} {분석} {모형} Table {만들기}},
date = {2024-09-13},
url = {https://blog.zarathu.com/posts/2024-09-13 jstable/},
langid = {en}
}